Basic Vector Operations with NumPy
Using Numpy in Preparation for Pytorch
Sources: 3b1b and https://github.com/ageron/handson-ml3/blob/main/math_linear_algebra.ipynb
Tags: Theory, Machine Learning
Vector Addition
Vectors can only be added if they are the same size. Addition is element-wise.
# Using lists
u = [1, 2, 3]
v = [3, 4, 5]
print(" ", u)
print("+", v)
print("-"*10)
print([v[i] + u[i] for i in range(len(u))])
import numpy as np
# Using numpy
u = np.array([2, 4])
v = np.array([9, 1])
print(" ", u)
print("+", v)
print("-"*10)
u + v
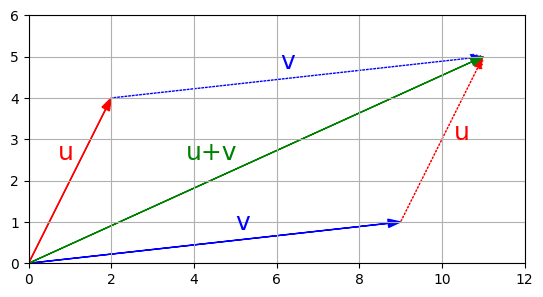
Figure 1. A visualization of vector addition
Subtracting a vector can be thought of as adding a negative vector.
Scalar Multiplication
(using Numpy) e.g. x * v = [...]
Dot Product
u • v = ||u|| * ||v|| * cos(θ), where θ is the angle between the vectors.
OR
u • v = (u1 * v1) + (u2 * v2) + ... + (uk * vk)
where u and v are vectors of length k.
For example, [2 4 6] • [2 4 6] = (2 * 2) + (4 * 4) + (6 * 6) = 4 + 16 + 36 = 56
# Using lists
u = np.array([2, 4, 6])
v = np.array([2, 4, 6])
dot_product = sum(ui * vi for ui, vi in zip(u, v))
print(dot_product)
# Using numpy
print(np.dot(v, u))
print(u.dot(v))
print(v.dot(u))
Norm
Equal to the square root of the sum of the squares of of all the components of u. Also equal to the square root of the dot product of u.
# Lists
u = [2, 5]
sum(ui ** 2 for ui in u) ** 0.5
# Numpy
np.linalg.norm(u)
Vector Normalization
A vector divided by its norm (i.e. a unit vector sharing the same direction as the original vector) is called a normalized vector.
Angle between vectors
θ = arccos(u • v / ||u|| * ||v||)
u = np.array([2, 5])
v = np.array([3, 1])
cos_theta = u.dot(v) / np.linalg.norm(u) / np.linalg.norm(v)
theta = np.arccos(cos_theta.clip(-1, 1))
print("Angle =", theta, "radians")
print(" =", theta * 180 / np.pi, "degrees")
Projection
The projection of vector v onto vector u is defined as:
(u • v) / ||u||2 * u
and can be thought of as laying v on top of u.
(u.dot(v) / np.linalg.norm(u) ** 2) * u
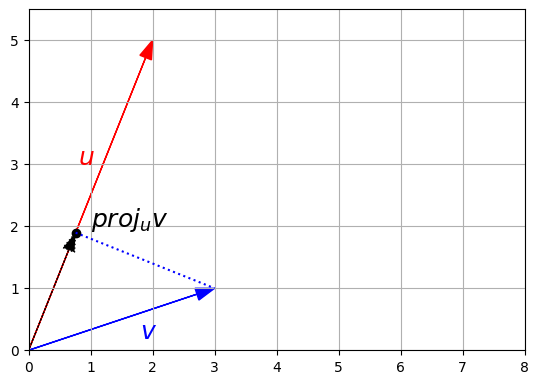
Figure 1. The projection of a vector v onto vector u